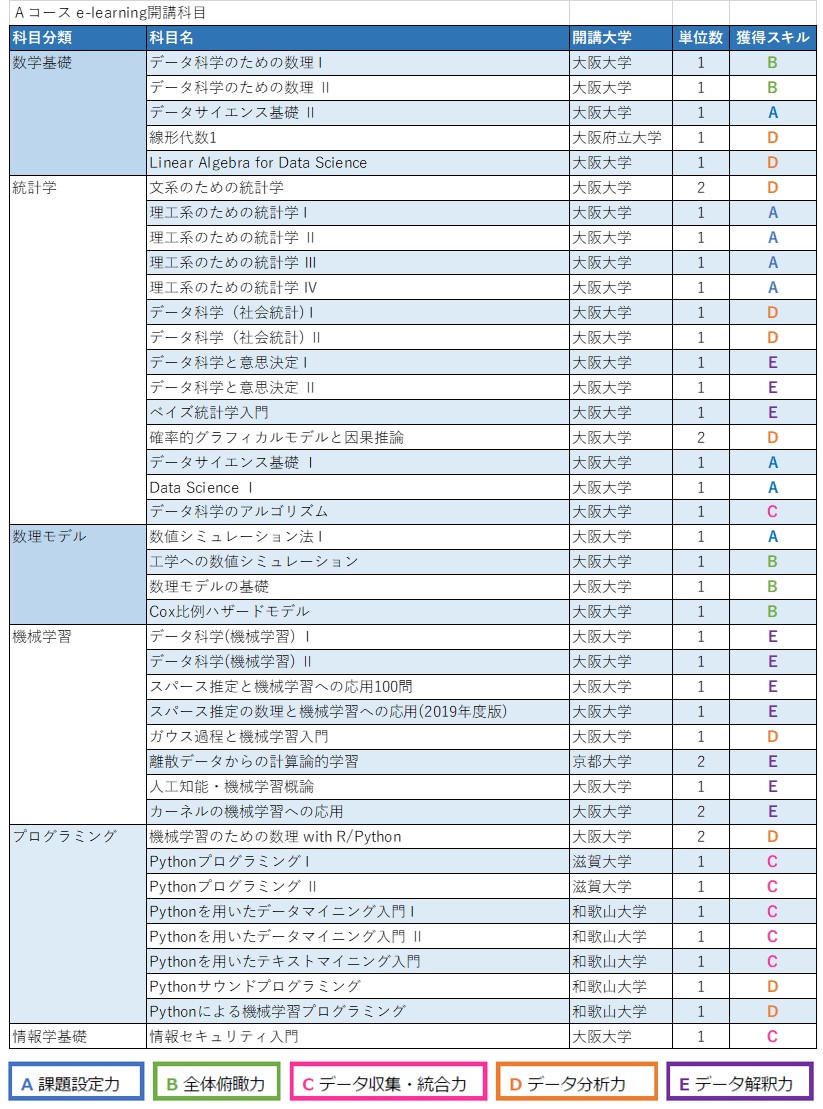
Aコース:データサイエンス『基礎コース』
Aコースで5単位を取得した受講生には、「基礎コース修了証」を発行します。
データサイエンティストが必要とされる知識・スキルを習得するためのコース。
データを価値に変換する際に必要な4つのプロセスである「データサイエンス全体俯瞰能力向上」「データ収集・統合」「データ分析」「データ解釈」を、e-Learningや大学講義を通じて学ぶことができます。
※ 受講を希望する方は各講義の募集期限をご確認の上、こちらの受講登録手順に従い、登録を行ってください。
※ 現段階で日程が未確定のものについては、詳細が決まり次第、掲載いたします。
※ (参考)前年度の講義内容はこちら
大阪大学講義
大阪大学キャンパスカレンダーはこちら
大阪大学シラバスはこちらのページの「大阪大学学務情報システム(KOAN)外部公開シラバス」から検索してください
- [科目名]
- 機械学習の数理 with R/Python
- [日程]
- 演習(e-Learning)
- 時間割コード
- 290850
- [募集期限]
2021年8月6日(金)正午※受付終了しました- [単位]
- 2単位
- [目的と概要]
- 機械学習の基礎を、数学的な側面、プログラミング的な側面の両側から習得する。
- 1.線形回帰(1)
- 2.線形回帰(2)
- 3.線形回帰(3)
- 4.ロジスティック回帰
- 5.線形判別と2次判別
- 6.クロスバリデーションとブートストラップ
- 7.情報量基準(1)
- 8.情報量基準(2)
- 9.スパース推定
- 10.非線形
- 11.決定木
- 12.サポートベクトルマシン(1)
- 13.サポートベクトルマシン(2)
- 14.クラスタリング
- 15.主成分分析
- [受講者へのメッセージ]
- e-Learningの形式になるので、ビデオをみて学習し、疑問点があれば質問し、課題を提出する。難しい課題は、丁寧すぎるくらいのヒントがついているので、すべて提出できるものと思われる。R言語の処理が読めることが前提となる。もし、R言語を勉強した経験がない場合、こちらでビデオを提供するので、それを見て習得するように心がける。
- [科目名]
- スパース推定の数理と機械学習への応用 with R/Python
- [日程]
- 演習(e-Learning)
- 時間割コード
- 290841
- [募集期限]
2021年8月6日(金)正午※受付終了しました- [単位]
- 2単位
- [目的と概要]
- スパース推定の基礎を、数学的な側面、プログラミング的な側面の両側から習得する。線形回帰、一般化線形回帰、グループLasso、グラフィカルLassoについて学ぶ。
- 1. 線形回帰(1) 理論
- 2. 線形回帰(2) 演習
- 3. 一般化線形回帰(1) 理論
- 4. 一般化線形回帰(2) 演習
- 5. グループLasso (1) 理論
- 6. グループLasso (2) 演習
- 7. グラフィカルLasso(1) 理論
- 8. グラフィカルLasso(2) 演習
- [受講者へのメッセージ]
- e-Learningの形式になるので、ビデオをみて学習し、疑問点があれば質問し、課題を提出する。
R言語の処理が読めることが前提となる。もし、R言語を勉強した経験がない場合、こちらでビデオを提供するので、それを見るとともに、習得するように心がける。
- [科目名]
- 確率的グラフィカルモデルと因果推論
- [日程]
- 演習(e-Learning)
- 時間割コード
- 290845
- [募集期限]
2021年8月6日(金)正午※受付終了しました- [単位]
- 2単位
- [目的と概要]
- 機械学習の分野のひとつ、確率的グラフィカルモデルと因果推論について学ぶ。
- 1. イントロダクション、応用事例
- 2. 条件付き独立性, 確率的グラフィカルモデル
- 3. データ圧縮
- 4. 相互情報量の推定
- 5. データから森を構築する
- 6. データからベイジアンネットワークを構築する
- 7. 変数が離散の場合
- 8. パラメータの事前分布
- 9. 変数が連続の場合
- 10. PCアルゴリズム
- 11. LINGAM
- 12. chordalグラフ
- 13. 確率推論のNP完全性
- 14. 推論アルゴリズムと統計物理
- 15. グラフィカルLasso
- [受講者へのメッセージ]
- R言語の処理が読めることが前提となる。もし、R言語を勉強した経験がない場合、こちらでビデオを提供するので、それを見て習得するように心がける。
- [科目名]
- カーネルの機械学習への応用
- [日程]
- 演習(e-Learning)
- 時間割コード
- 290862
- [募集期限]
2021年8月6日(金)正午※受付終了しました- [単位]
- 2単位
- [目的と概要]
- 機械学習のためのカーネルの数理について講義する。サポートベクトルマシン、独立性検定、ガウス過程、ベイズ深層学習など、応用範囲が広い。
- 1. 関数解析入門
- 2. 関数解析発展
- 3. 正定値カーネル
- 4. 再生核ヒルベルト空間入門
- 5. 再生核ヒルベルト空間発展
- 6. HSIC(1) 平均の概念の導入
- 7. HSIC(2) 独立性検定
- 8. ガウス過程(1) 定義と性質
- 9. ガウス過程(2) ガウス過程の計算とスパース近似
- 10. ソボレブ空間
- 11. スプライン関数
- 12. 多変量解析
- 13. 多変量解析の関数解析的な取り扱い
- 14. ラドマッハ複雑度とVC次元
- 15. 経験過程と機械学習への応用
- [受講者へのメッセージ]
- ノートパソコンを持参のこと。R言語またはPythonを習得していない場合、最短で習得するビデオを提供する。
- [科目名]
- 多変量解析
- [日程]
- 2021年10月5日~
- [募集期限]
2021年8月6日(金)正午※受付終了しました- [単位]
- 2単位
- [目的と概要]
- 多変量解析は互いに関連した複数個の観測項目のデータ(多変量データ)から、項目間の因果関係を検討したり、内部構造を解明したりするための統計的方法論である。
- 本講義では、まず、多変量解析の各種手法が理解できるための数理的基礎を固める。つづいて、多くの統計分析手法の基礎となる回帰分析を講述する。実際例と注意すべき点、変数選択や数理的基礎を紹介する。次に、任意の統計モデルにおいて生じる欠測値問題を講述する。
- 序
- 第 1回 多変量解析とは
- 復習と準備
- 第 2回 線形代数の復習
- 第 3回 射影行列とCochranの定理
- 第 4回 分割行列,Woodbury's identity, Katri's lemma, Duplication matrix
- 第 5回 確率分布の復習
- 第 6回 条件付き期待値と最小二乗法
- 第 7回 収束定理
- 回帰分析:概説編
- 第 8回 概説編1:実例,偏回帰係数の機能とその解釈,様々な検定とそれら関係
- 第 9回 概説編2:回帰診断
- 第10回 非線形回帰の妙(多項式回帰)
- 第11回 非線形回帰の妙(Gaussian Process)
- 回帰分析:理論編
- 第12回 統計理論の概要1: BLUE, Lehmann-Scheffe の定理
- 第13回 統計理論の概要2: Rao-Blackwellの定理,Cramer-Rao の定理
- 第14回 統計理論の概要3: 一致性と漸近分布,科学的精密実験と回帰分析
- 応用的な話題
- 第15回,第16回 以下のトピックの中から選択して講述する
- ロジスティック回帰分析、線型対数モデル、分類と判別、欠測データの解析、統計的因果推論、因子分析の概要と基礎、等からいくつかを選択して講述予定
- [受講者へのメッセージ]
- 初等統計学、線形代数学と初等解析学の知識があることが望ましい。
- 他領域からの受講生も歓迎する。数理を専門としない受講生に配慮する。
- [科目名]
- データ科学(機械学習)
- [日程]
- 2021年10月5日~
- [募集期限]
2021年8月6日(金)正午※受付終了しました- [単位]
- 2単位
- [目的と概要]
- 膨大な実世界データから有益な情報を知識として抽出し、それを再利用した人工システムを設計するためには、機械学習の枠組みが有効である。本講義では、その数学の理論およびアルゴリズムを俯瞰しながら機械学習の基礎を講義する。学生は機械学習にて必要な統計・最適化理論およびそれを形にするアルゴリズムの基礎を習得することができる。
- 第1回目 統計数理の復習(正規分布,相関,ベイズの定理)
- 第2回目 数理最適化の復習(数理計画,動的計画問題)
- 第3回目 データの特徴抽出・低次元化(主成分分析,カーネル主成分分析,判別分析)
- 第4回目 統計的回帰分析
- 第5回目 観測データからの非観測状態の推定(カルマンフィルタ)
- 第6回目 観測データからの非観測状態の推定2(パーティクルフィルタ)
- 第7回目 非観測状態の推定とモデル最適化(EMアルゴリズム)
- 第8回目 非観測状態の推定とモデル最適化(EMアルゴリズム2)
- 第9回目 統計的生成モデルの機械学習(混合ガウスモデル)
- 第10回目 統計的生成モデルの機械学習2(隠れマルコフモデル)
- 第11回目 統計的識別モデルの機械学習(サポートベクターマシン)
- 第12回目 統計的識別モデルの機械学習2(コンディショナルランダムフィールド)
- 第13回目 統計的生成モデルと識別モデルの統合(フィッシャベクトル)
- 第14回目 ニューラルネットワークの機械学習
- 第15回目 機械学習の実際:ロボットの運動への適用
- [受講者へのメッセージ]
- 講義ページにアップロードされている講義ノートを活用しながら、授業中にわからなかったことを復習して理解を補足すること。
- [科目名]
- データ科学と意思決定
- [日程]
- 2021年10月4日~
- [募集期限]
2021年8月6日(金)正午※受付終了しました- [単位]
- 2単位
- [目的と概要]
- 我々の日常の営みは意思決定の連続です。また,医療診断,株式投資,企業判断そして政策立案など様々な社会活動において,適切な意思決定のあり方が問題とされます。本講義では,データ科学の理論的な枠組みから意思決定プロセスをモデル化する方法,および脳認知科学の知見を踏まえたヒトの意思決定の特性を講述し,よりよい意思決定を導くための方略について議論します。
- 意思決定とそのモデルについての概要
- 1.意思決定課題の分類 適用される分野
- 統計的決定の基礎
- 2.ベイズ推定 損失関数
- 3.信号検出理論:信号の弁別度
- 4.信号検出理論:ROC解析
- 5.決定課題としての検定問題
- ヒトの意思決定の特性
- 6.知覚・運動における意思決定
- 7.ウェイソン選択課題(4枚カード問題)
- 8.帰納的推論
- 9.確率推定
- 意思決定理論
- 10.ベイジアンネットワーク
- 11.選択公理と強化学習
- 12.効用理論 プロスペクト理論
- 意思決定の脳認知科学
- 13.情動・感情・リスク評価の役割
- 14.直感と熟考の機能
- 15.意思決定の脳内基盤
- [受講者へのメッセージ]
- E-learning教材を活用し,事前学習と復習を行う。
- [科目名]
- 工学への数値シミュレーション
- [日程]
- 2021年10月6日~
- [募集期限]
2021年8月6日(金)正午※受付終了しました- [単位]
- 2単位
- [目的と概要]
- 有限要素法は理工学分野で広く使われている数値計算手法である一方,そのアルゴリズムを理解することがしばしば困難になる場合もある。
- 本講義では,下記の項目に挙げる,有限要素法を使った数値計算を確実に使えるようになるための最低限の内容を学習するとともに,工学分野で必要とされる技術を身に着ける。
- 各自が持参したノートパソコンを使って数値計算を行う
- ・講義内で指定する有限要素法を用いた数値計算に必要な最低限の学習
- ・工学分野で用いられる技術の習得
- 1.ガイダンス
- 2.数値計算の準備(最低限の線形代数・ベクトル解析・微分積分の復習)
- 3.ソフトウェアのインストール
- 4.数値計算1 メッシュ生成の説明と演習
- 5.数値計算2 ポアソン方程式の数値計算
- 6.数値計算3 変分問題の基本概念
- 7.数値計算4 拡散方程式の数値計算
- 8.数値計算5 移流方程式の数値計算
- 9.数値計算6 移流・拡散方程式の数値計算
- 10.数値計算7 Stokes方程式の弱形式の導出
- 11.数値計算8 Navier-Stokes方程式の数値計算
- 12.数値計算9 2次元翼断面の数値シミュレーション
- 13.数値計算10 線形安定性解析の説明と数値計算
- 14.数値計算11 Snapshot PODの説明と数値計算
- 15.数値計算12 Dynamic Mode Decomposition説明と数値計算
- [受講者へのメッセージ]
- 各自のノートパソコンに有限要素法で計算するための無償のソフトウェア(ガイダンスで指定)をインストールしておくこと。
- [科目名]
- 機械学習の実践
- [日程]
- 2021年10月6日~
- [募集期限]
2021年8月6日(金)正午※受付終了しました- [単位]
- 2単位
- [目的と概要]
- 確率論と情報理論に基づいた機械学習の理論を学ぶ。画像解析、時系列解析、教師なし学習などに用いられる深層学習(ディープラーニング)のモデルについて学ぶ。
- 扱う内容:各トピックを約3回ずつでカバーする予定。授業の進行に応じて、扱い方やトピックを変更することがある。
- 確率論・情報理論
- ベイズ推論と機械学習
- ニューラルネットワークの学習
- 深層学習(ディープラーニング)の確率モデル
- 強化学習
- [受講者へのメッセージ]
- 大学1年生の講義で扱われる程度の、初等的な確率論の知識(確率変数、確率密度関数など)、微積分の知識(偏微分など)、線形代数の知識(行列の計算など)を用いる。
- [参考文献]
- 講義で扱う内容に深く関係する参考書として、
瀧雅人「これならわかる深層学習入門」機械学習スタートアップシリーズ、講談社、2017
須山敦志「ベイズ推論による機械学習入門」機械学習スタートアップシリーズ、講談社、2017
神戸大学講義
神戸大学キャンパスカレンダーはこちら
神戸大学シラバスはこちら
- [科目名]
- データサイエンス特論1
- [日程]
- 集中講義 2021年11月10~12日
- [募集期限]
2021年10月14日(木)※受付終了しました- [単位]
- 1単位
- [目的と概要]
- 第4次産業革命において、IoT、AI(人工知能)、ビッグデータの利用が鍵となり、データサイエンスが新しい学問分野、技術分野として注目されている。この講義では、データサイエンスの基礎である人工知能・機械学習の技術的側について学ぶ。
大阪府立大学講義
大阪府立大学キャンパスカレンダーはこちら
大阪府立大学シラバスはこちら
- [科目名]
- ナレッジマネジメント特論
- [日程]
- 水・5限
- [募集期限]
2021年9月8日(水)※受付終了しました- [単位]
- 1単位
- [目的と概要]
- この講義では、ナレッジマネジメントをはじめとして、生産から経営まで企業を取り巻く社会環境および意思決定に役立ついくつかの手法を幅広く学習する。まずナレッジマネジメントについて概要を述べたあと、企業の組織と業務遂行に必要な情報伝達について触れる。企業間情報ネットワークやERPなどのハードとソフト面における情報の利活用について説明する。また、意思決定に役立つロジスティック回帰分析およびゲーム理論についても講義する。
- なお、授業は対面形式(コロナの状況によりオンラインに変更の可能性あり)にて実施します。
- [科目名]
- データサイエンス特論
- [日程]
- 金・3限
- [募集期限]
2021年9月8日(水)※受付終了しました- [単位]
- 1単位
- [目的と概要]
- データサイエンスで中心的な役割を果たす機械学習について、その基礎知識を学ぶ。実際に機械学習を用いる場合に必要となる技術である前処理やモデル選択などを学習する。また、代表的な機械学習手法のアプローチであるベイズ学習とカーネル法について学習する。
各協定校
- 問い合わせ先
- こちらのお問い合わせフォームからお願いします。